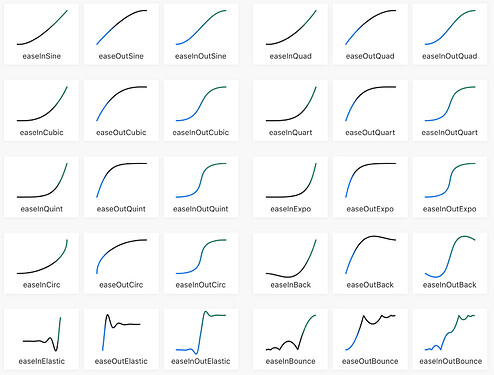
Continuing the discussion from Smooth Speed Slider?:
This isn’t quite right, the last few don’t look correct, so I’m sure I need to play with them, but most of these seem right, based on the demo results.
Likely, I’ll add some additional demos to this as well.
what these should look like:
My demo doesn’t yet match those curves (TBD), but I do have consistent curves, so…
Posting so that this gets some fresh eyeballs, and if someone spots the goof(s), let me know, and save me some debugging time. I’m thinking the last ones need to handle lower/higher than 0…1 values (in my demo that is, I suspect it’s correct for the library code to do that).
/**
* Easing library by ScruffyNerf v0.9 May 2021
* based on info from https://easings.net (see the images there for an example curve for each function)
* To use as a library, add the easing functions you wish to use to your own patterns
* All take a 0..1 value, and return a 0..1 value
*/
// Library
// Constants used
var c1 = 1.70158;
var c2 = c1 * 1.525;
var c3 = c1 + 1;
var c4 = (PI2) / 3;
var c5 = (PI2) / 4.5;
function easeInSine(x){
return 1 - cos((x * PI) / 2);
}
function easeOutSine(x){
return sin((x * PI) / 2);
}
function easeInOutSine(x){
return -(cos(PI * x) - 1) / 2;
}
function easeInQuad(x) {
return x * x;
}
function easeOutQuad(x) {
return 1 - (1 - x) * (1 - x);
}
function easeInOutQuad(x) {
return x < 0.5 ? 2 * x * x : 1 - pow(-2 * x + 2, 2) / 2;
}
function easeInCubic(x) {
return x * x * x;
}
function easeOutCubic(x) {
return 1 - pow(1 - x, 3);
}
function easeInOutCubic(x) {
return x < 0.5 ? 4 * x * x * x : 1 - pow(-2 * x + 2, 3) / 2;
}
function easeInQuart(x) {
return x * x * x * x;
}
function easeOutQuart(x) {
return 1 - pow(1 - x, 4);
}
function easeInOutQuart(x) {
return x < 0.5 ? 8 * x * x * x * x : 1 - pow(-2 * x + 2, 4) / 2;
}
function easeInQuint(x) {
return x * x * x * x * x;
}
function easeOutQuint(x) {
return 1 - pow(1 - x, 5);
}
function easeInOutQuint(x) {
return x < 0.5 ? 16 * x * x * x * x * x : 1 - pow(-2 * x + 2, 5) / 2;
}
function easeInExpo(x) {
return x == 0 ? 0 : pow(2, 10 * x - 10);
}
function easeOutExpo(x) {
return x == 1 ? 1 : 1 - pow(2, -10 * x);
}
function easeInOutExpo(x) {
return x == 0 ? 0 : x == 1 ? 1 : x < 0.5 ? pow(2, 20 * x - 10) / 2 : (2 - pow(2, -20 * x + 10)) / 2;
}
function easeInCirc(x) {
return 1 - sqrt(1 - pow(x, 2));
}
function easeOutCirc(x) {
return sqrt(1 - pow(x - 1, 2));
}
function easeInOutCirc(x) {
return x < 0.5 ? (1 - sqrt(1 - pow(2 * x, 2))) / 2 : (sqrt(1 - pow(-2 * x + 2, 2)) + 1) / 2;
}
function easeInBack(x) {
return c3 * x * x * x - c1 * x * x;
}
function easeOutBack(x) {
return 1 + c3 * pow(x - 1, 3) + c1 * pow(x - 1, 2);
}
function easeInOutBack(x) {
return x < 0.5 ? (pow(2 * x, 2) * ((c2 + 1) * 2 * x - c2)) / 2
: (pow(2 * x - 2, 2) * ((c2 + 1) * (x * 2 - 2) + c2) + 2) / 2;
}
function easeInElastic(x) {
return x == 0 ? 0 : x == 1 ? 1 : -pow(2, 10 * x - 10) * sin((x * 10 - 10.75) * c4);
}
function easeOutElastic(x) {
return x == 0 ? 0 : x == 1 ? 1 : pow(2, -10 * x) * sin((x * 10 - 0.75) * c4) + 1;
}
function easeInOutElastic(x) {
return x == 0 ? 0 : x == 1 ? 1 : x < 0.5
? -(pow(2, 20 * x - 10) * sin((20 * x - 11.125) * c5)) / 2
: (pow(2, -20 * x + 10) * sin((20 * x - 11.125) * c5)) / 2 + 1;
}
function easeInBounce(x) {
return 1 - easeOutBounce(1 - x);
}
function easeOutBounce(x) {
n1 = 7.5625;
d1 = 2.75;
if (x < 1 / d1) {
return n1 * x * x;
} else if (x < 2 / d1) {
return n1 * (x -= 1.5 / d1) * x + 0.75;
} else if (x < 2.5 / d1) {
return n1 * (x -= 2.25 / d1) * x + 0.9375;
} else {
return n1 * (x -= 2.625 / d1) * x + 0.984375;
}
}
function easeInOutBounce(x) {
return x < 0.5 ? (1 - easeOutBounce(1 - 2 * x)) / 2 : (1 + easeOutBounce(2 * x - 1)) / 2;
}
// end library
// begin demo
demofunctions = 30
var demo = array(demofunctions)
demo[0] = (x) => easeInSine(x)
demo[1] = (x) => easeOutSine(x)
demo[2] = (x) => easeInOutSine(x)
demo[3] = (x) => easeInQuad(x)
demo[4] = (x) => easeOutQuad(x)
demo[5] = (x) => easeInOutQuad(x)
demo[6] = (x) => easeInCubic(x)
demo[7] = (x) => easeOutCubic(x)
demo[8] = (x) => easeInOutCubic(x)
demo[9] = (x) => easeInQuart(x)
demo[10] = (x) => easeOutQuart(x)
demo[11] = (x) => easeInOutQuart(x)
demo[12] = (x) => easeInQuint(x)
demo[13] = (x) => easeOutQuint(x)
demo[14] = (x) => easeInOutQuint(x)
demo[15] = (x) => easeInExpo(x)
demo[16] = (x) => easeOutExpo(x)
demo[17] = (x) => easeInOutExpo(x)
demo[18] = (x) => easeInCirc(x)
demo[19] = (x) => easeOutCirc(x)
demo[20] = (x) => easeInOutCirc(x)
demo[21] = (x) => easeInBack(x)
demo[22] = (x) => easeOutBack(x)
demo[23] = (x) => easeInOutBack(x)
demo[24] = (x) => easeInElastic(x)
demo[25] = (x) => easeOutElastic(x)
demo[26] = (x) => easeInOutElastic(x)
demo[27] = (x) => easeInBounce(x)
demo[28] = (x) => easeOutBounce(x)
demo[29] = (x) => easeInOutBounce(x)
export var timeelapsed
export var currentdemo = 0
export function beforeRender(delta) {
timeelapsed += delta
if (timeelapsed >= 3000){
timeelapsed = 0
currentdemo += 1
if (currentdemo == 30){
currentdemo = 0
}
}
}
export function render(index) {
h = demo[currentdemo](index/pixelCount)
s = 1
v = 1
hsv(h, s, v)
}
export function render2D(index,x,y){
h = demo[currentdemo](x)
s = 1
v = 1
if (demo[currentdemo](y) <= x){
hsv(h, s, v)
} else {
hsv(0, 0, 0)
}
}