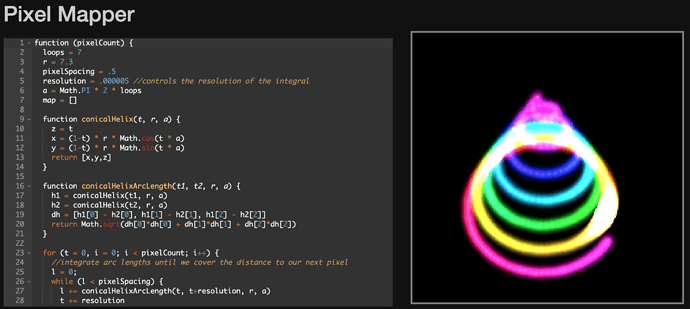
Thats a bit harder. Its tempting to do something like Mapping a Helix except the radius shrinks or grows with the for loop’s i variable, but the pixel distance gets messed up.
I turned to a bit of googling and calculus. Found the formula for a conical helix, and then integrating to find the arc distance to space out pixels. I don’t have time to dig further to figure out how to find the radius and spacing to match a specific number of pixels given 7 loops, but it’s easy to play with the numbers until things get really close.
function (pixelCount) {
loops = 7
r = 7.3
pixelSpacing = .5
resolution = .000005 //controls the resolution of the integral
a = Math.PI * 2 * loops
map = []
function conicalHelix(t, r, a) {
z = t
x = (1-t) * r * Math.cos(t * a)
y = (1-t) * r * Math.sin(t * a)
return [x,y,z]
}
function conicalHelixArcLength(t1, t2, r, a) {
h1 = conicalHelix(t1, r, a)
h2 = conicalHelix(t2, r, a)
dh = [h1[0] - h2[0], h1[1] - h2[1], h1[2] - h2[2]]
return Math.sqrt(dh[0]*dh[0] + dh[1]*dh[1] + dh[2]*dh[2])
}
for (t = 0, i = 0; i < pixelCount; i++) {
//integrate arc lengths until we cover the distance to our next pixel
l = 0;
while (l < pixelSpacing) {
l += conicalHelixArcLength(t, t+resolution, r, a)
t += resolution
}
map.push(conicalHelix(t, r, a))
}
return map
}