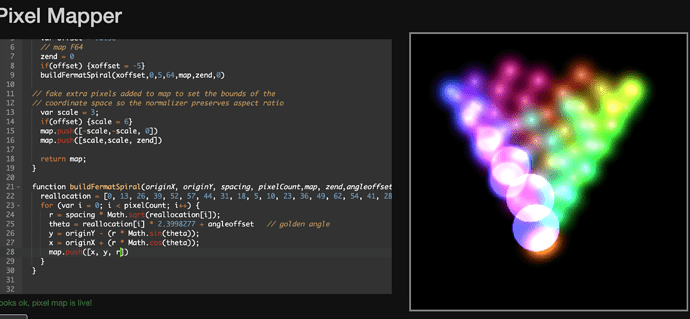
ok almost perfect
I had to rotate some of the angle offsets, but also invert the y on one of the F64s.
There’s just one pixel a bit off. the center pixel in the left F64, it’s a little early in blue and a little late on green. Any ideas?
function (pixelCount) {
var map = []
var zend = 0
var xoffset = 0
var offset = false
var angleOffset = 0
var cone = 0
var isFirst = true
// map F64
zend = -60
if(offset) {xoffset = -5}
angleOffset = 3 //###########################
cone = 1
buildFermatSpiral(xoffset,0,.10,64,map,zend,angleOffset,cone,isFirst)
// map helix connecting
var helixCount = (pixelCount-128);
zend = 20
angleOffset = 3 //###########################
count = helixCount/2
zend = buildHelixMap(helixCount, map,zend,angleOffset,count)
zend = zend + 10
angleOffset = 2 //###########################
zend = buildHelixMap(helixCount, map,zend,angleOffset,count)
// map F64
if(offset) {xoffset = 5}
angleoffset = 0 //###########################
cone = -1
isFirst = false
buildFermatSpiral(xoffset,0,.10,64,map,zend+60,angleoffset,cone,isFirst)
// fake extra pixels added to map to set the bounds of the
// coordinate space so the normalizer preserves aspect ratio
var scale = 2;
if(offset) {scale = 6}
map.push([-scale,-scale, -60])
map.push([scale,scale, zend+120])
return map;
}
function buildFermatSpiral(originX, originY, spacing, pixelCount,map, zend, angleOffset, cone, isFirst) {
reallocation = [0, 13, 26, 39, 52, 57, 44, 31, 18, 5, 10, 23, 36, 49, 62, 54, 41, 28, 15, 2, 7, 20, 33, 46, 59, 51, 38, 25, 12, 4, 17, 30, 43, 56, 61, 48, 35, 22, 9, 1, 14, 27, 40, 53, 58, 45, 32, 19, 6, 11, 24, 37, 50, 63, 55, 42, 29, 16, 3, 8, 21, 34, 47, 60]
for (var i = 0; i < pixelCount; i++) {
r = spacing * Math.sqrt(reallocation[i]);
theta = reallocation[i] * 2.3998277 + angleOffset // golden angle
if(isFirst) {
y = originY + (r * Math.sin(theta));
} else {
y = originY - (r * Math.sin(theta));
}
x = originX + (r * Math.cos(theta));
map.push([x, y, (cone*r*r*50)+zend])
}
}
function buildHelixMap(pixelCount,map,zend,angleOffset,count) {
var loops = 12
var helixCount = (pixelCount-128);
var rowCount = helixCount/35;
var lastZ = 0;
for (i = 0; i < count; i++) {
c = i / pixelCount * Math.PI * 2 * loops
c = c + angleOffset
lastZ = (i/rowCount) + zend;
map.push([Math.cos(c), Math.sin(c), lastZ])
}
return lastZ;
}