Mapping Complex Objects

[Sunandmooncouture]

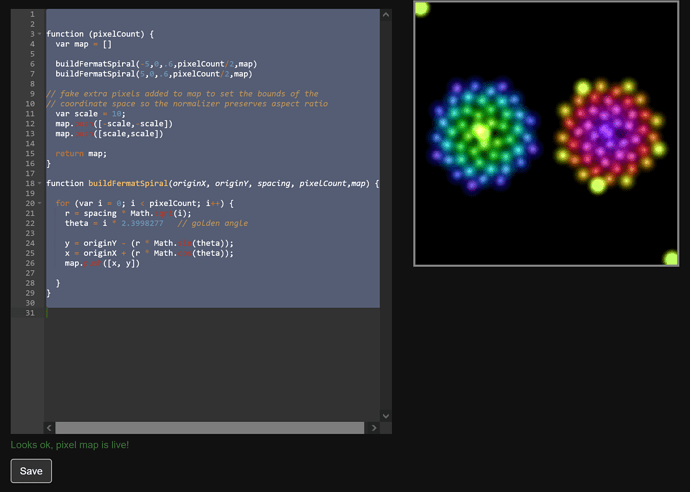
so I’m building a new mask using Jason Coon’s amazing Fibonacci 64 LED PCB on the face plate. The last version was using concentric rings which mapped fairly easily with if(index > X && index < y) with start/end of each ring.

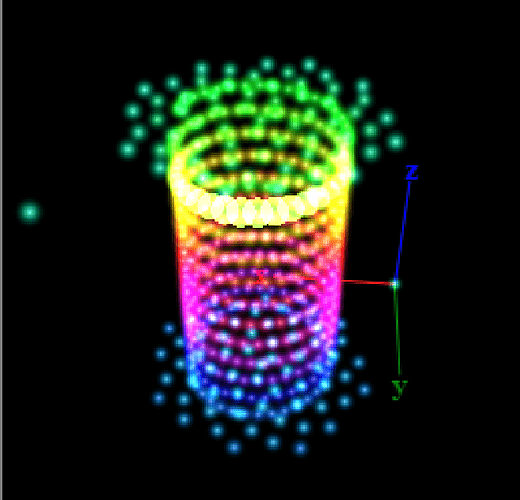
Here’s a picture of the completed mask for reference.

The new F64 itself could be mapped easily enough in the online tool.

The strips spiraled around the sides of the can would be easy to map mathematically themselves.

Combining both of these different objects into a single map seems impossible.
I bet Jason or someone smarter than me could figure out the calculus to describe both of these object perfectly mathematically, but it’s beyond me.

I also tried mapping the F64 into concentric-ish rings, which might be like trying to fit a spiral peg into a round hole.

But even just creating the arrays to contain the indexes of each ring, and checking if the current pixel was in a specific ring ends up dropping FPS to 7ish. I could maybe use help with optimizing that code too. Or should I give up?

My main question is - Is this even doable and should I even try to attempt mapping something like this?

Another complication is wanting different maps for different patterns, so I’m trying to do the mapping in the pattern, not the map tab.

e.g. the concentric rings map would be nice for a sound pattern to show the energyAverage light up each concentric ring as the volume increases, eventually lighting up rows of the spiral round the sides.

But it would also be interesting to see each of the “columns” of 5 leds in the F64 light up as a separate frequency meter, with 5 lines of resolution. but I have no idea how that would extend to strips on the side.

I’m open to suggestions including demoralizing criticism.

[jeff]

Hey Anthony! Happy to help optimize code for efficiency (I’ve done some radial projects where I sometimes want it polar: specify a radial or radius) or sometimes Cartesian.

First, I was wondering if you’ve seen/snagged the F64 maps Jason provided on his site? Then adding the sides as a 3D cylinder might be more approachable:

https://www.evilgeniuslabs.org/fibonacci64#pixelblaze-maps

To help with efficiency, maybe you pick and use one primary mapping in the map tab, and the have a transform from there when you want to access it a different way.

[Sunandmooncouture]

“F64 maps Jason provided on his site”

Okay, I’ll be back later with better questions. Thanks!

[Scruffynerf]

Given the layout, you’d be best served with a Cylindrical 3D map, for sure.
If you imagine the center of the spiral as the top of the cylinder, then the radius increases, till the radius matches your outer rings. The depth of the spiral is all 0, then the rings get depth values (height), and then the angle is the 3rd axis. (so you just have to measure the angle of each led in the spiral, from a given center line)

so R,H, and A.

Once you have it in one format, you can write a pattern to convert it to X,Y,Z, and then install that as the default map if you wish, so ‘normal’ 3D patterns would work, BUT…
Polar patterns (R/A) will look awesome on this (we need more of them, it’s on my todo list). And then if you want to do something with just the rings, you can limit to values of H higher/lower (whichever you prefer) than zero. Rings on the spiral, are ranges of R, btw, so between those two, you should reduce your checks to minimal for FPS purposes.

In case that’s not clear, a rough example…
first ring R>.2
second ring R> .4
third ring R>.6
etc…
if the outer rings are all at R = 1, then each ring there is the H>.2, H>.3,H>.4 etc…
So that’ll give your frequency meter, strength via rings, then the actual frequencies, that’s angle… divide by 32 buckets (or less likely), and you’re all set. That won’t quite give you the spiral, but nudging the angle a bit as you increase the strength will likely do it. (When you get there, happy to help fine tune it)

And of course, you can mirror these (left and right), OR go for the big super full map, and map it all in a 3D space… but I suspect most times, mirroring will look better.

EXCEPT, I just realized that the spirals all going in the same direction, so it’s NOT a perfect mirror, but if you map it as a cylinder, the same on both, it’ll mirror anyway.
Ignore that, it’s close enough mirror, the pattern will look good even if the panel isn’t exact (it’s ‘handed’, @JasonCoon doesn’t make both left and right versions, which would be mirrors. Right, Jason?.. you can light up the counter clockwise spirals once it’s mapped right.

Ah, Jason’s provided map is XYA… with XY, you can calculate R (hypot(X,Y) but that’s expensive), and you could fake H by just considering it a bigger R (imagine R is a tape measure that goes from the center of the spiral, to the edge, then runs down the rings.)

One more reason it would be nice to have a 4th axis in the map

[Scruffynerf]

The math:

The fabulous Fibonacci flower formula

here’s a non-math-y way that makes it clear, and why it’s 137.5 degree apart each time

Fibonacci Flower

(so it’s a spiral, with 137.5 (or a fraction thereof) between each led, and a slight increase in radius each time.)

The actual math:
angle = n ∗ 137.5, r = c√n

n is the number of the leds, not as wired, but counting outward from center) and c contributes to a scaling factor.
Since this formula gives an angle and radius, we can convert it to x and y by using Polar Coordinates (r,θ) to Cartesian Coordinates (x,y) transformation
x = r * cos(angle); y = r * sin(angle)

[Sunandmooncouture]

Okay so I’m looking at the link posted for the F64 maps.
It mentions a 2D XY map which I already had using the online mapping tool.
It also mentions a 2D Polar map which I don’t see on the site anywhere.
Instead there’s a section labeled “Pixelblaze XY & Angle Map” but it seems to have XYZ coords for a 3D map that makes no sense to me.
Am I missing something?

[jeff]

Sounds like the polar map might just be missing. If you need this, you could email Jason – maybe it’s just missing a link. You can also compute the polar map yourself in JavaScript, by transforming the 2D XY map coordinates to find angle and radius for each pixel instead, and store that as the map.

For the “Pixelblaze XY & Angle Map”, the third dimension (v) will contain the angle from the center to that pixel instead of an actual z coordinate. This saves you from the computation effort in your render2D(). It’s redundant though - you could also get the angle from computing atan2(y,x). You wouldn’t use this map if you also needed Z to store the depth of the pixels on the spiraled sides of the cans and planned to use 3D patterns with it.

See here for how to map the helix spiral around the cans. You’ll append or prepend that helix maps with the Z component to the 2D map you got from the mapping tool or Jason’s site. You’ll add a third dimension to all the 2D coordinates for the F64, probably just defining z == 0 as the plane of the F64. So if the provided map looked like:

[[231, 98], [9, 33], ...
You’d use a text editor or some JS to turn it into:
[[231, 98, 0], [9, 33, 0], ...

Does that make sense?

As for inferring things about each pixel’s position within the spiral radial arms in the Fibonacci 64, you’ll need to define helper functions that takes a pixel index, and returns the ordinal number for which radial that pixel is on. For example, if there’s an even 7 pixels in each curved radial, it could be as easy as:

function arm(index) {
  return floor(index / 7)
}

And since it’s wired zig-zag in-out, you can build on this arm() function to convert index into the distance from the middle along this arm (in units of pixels):

function distFromCenter(index) {
  var distance = index % 7
  if (arm(index) % 2 == 0) {
    return distance
  } else {
    return 6 - distance
  }
}

Something like that. Is this getting you closer?

[Scruffynerf]

Sorry, thought I was clearer above:

Jason provided a XY-Angle map, X, Y, A.

I agree with Jeff, you can calc the angle from atan2, but I suspect calcing the R is slower (hypot)…

Regardless, providing the X, Y is half the work. You could do as Jeff says and wipe the angle into zeros and call it Z, and add the rings. Use the map formula for a cylinder/rings for those, and thatll add Z to them.

Jason’s examples show how he’s using X and Y to do wipes across the face of the disc.

We’ll make sure you have the map right in the end. There are options, and picking the best means picking the fastest for your desired patterns. That’s why I said more than 3 would be useful. Until @wizard provides it, though, you can calc whatever’s missing when needed. It’s just a speed issue. Given XYZ, you can run out of the box 3D patterns. But for your sound stuff, that’ll be awkward and slow to do rings, if you are calcing R constantly.

Maybe do it once on start, and caching it, I have code for that approach on here somewhere. (I’ll link it later). You build an R cache on pattern start, so you don’t have to keep calcing it. You could even do multiple caches including Jeff’s arm idea, and pick which is useful.

[JasonCoon]

Hey, sorry I’m late to the party!

As I’ve said in our emails, I love the mask @Sunandmooncouture!

Yes, the map on my site is XY & Angle [x,y,a]. I can easily make and post any other maps you might like. I have a spreadsheet with XY, angle, radius, etc here: Fibonacci64 Map - Google Sheets

I love Pixelblaze, but honestly still haven’t used it much. In Arduino/C, I just have arrays to map from physical index (the way they’re wired) to all of the different dimensions: esp8266-fastled-webserver/Map.h at fibonacci64 · jasoncoon/esp8266-fastled-webserver · GitHub
For all of my Fibonacci discs, physicalToFibonacci is really just a radius map.

If you’re limited to “only” three dimensions with Pixelblaze, I’ll defer to others who know more about it to help you decide which to use.

[Scruffynerf]

@JasonCoon

If you’re limited to “only” three dimensions with Pixelblaze, I’ll defer to others who know more about it to help you decide which to use.

Oh the spreadsheet is perfect. Until we convince @wizard to open up the multiverse of 4D or 5D, we can always just cache the other dimensions, and read them from an array. Can’t use the new transformation API as easily either. (Though if he does add more, that’ll require API changes too.)

We’ll just have to make PB irresistible for you, Jason. It’s getting there, as we flesh out all of the user libraries of effects and math.

[JasonCoon]

I just added a Pixelblaze map for [radius, angle] to the spreadsheet: Fibonacci64 Map - Google Sheets

[[0,0],[53,249],[105,241],[158,232],[210,223],[231,200],[178,208],[125,217],[73,226],[20,235],[40,212],[93,203],[146,194],[198,185],[251,176],[219,162],[166,171],[113,180],[61,188],[8,197],[28,174],[81,165],[134,156],[186,147],[239,139],[206,124],[154,133],[101,142],[49,151],[16,136],[69,128],[121,119],[174,110],[227,101],[247,78],[194,86],[142,95],[89,104],[36,113],[4,99],[57,90],[109,81],[162,72],[215,63],[235,40],[182,49],[130,58],[77,67],[24,75],[45,52],[97,43],[150,34],[202,25],[255,17],[223,2],[170,11],[117,20],[65,29],[12,38],[32,14],[85,6],[138,255],[190,246],[243,237]]

I tested it with this pattern code:

export function render2D(index, x, y) {
  t1 = time(0.02)
  hsv(x + t1, 1, 1)
}

And got a pattern very similar to this:

Just swapping y for x in that code:

export function render2D(index, x, y) {
  t1 = time(0.02)
  hsv(y + t1, 1, 1)
}

Gives this pattern:

[wizard]

Love the photography setup you have, do you keep that ready to shoot on a whim, @JasonCoon ?

@Sunandmooncouture ,
Depending on what you want to do, it’s easy to get angle from x,y using atan2, and radius using hypot or hypot3, and fast enough to not worry about it. In general I’d recommend that multiple pixel maps aren’t needed, but instead use a regular Cartesian x,y,z and calculate polar coordinates as needed. As @Scruffynerf has shown, sometimes caching these can help with speed if there are heavy map calculations.

With a bit of coordinate transformation, the Fibonacci disc can be added to the top of a cylinder. You could walk Jason’s 2d map and add a fixed z offset. I would be tempted to add some z to it based on the radius so it was modeled like a cone, then wipe effects would go up the cylinder and inward on the disc.

Do you intend to have both sides mapped, or mirroring data?

[Scruffynerf]

@wizard

, do you keep that ready to shoot on a whim

I’m pretty sure these are the same images he already had, and the new display was close enough to match.

I agree, adding a bit of Z to the disc makes sense, so the pixels “rise” in the center, and drop down towards the rings below the disc. In fact, that’s the cheat: make each ring a different Z value… So ring/Z 0 is the center, ring/Z 1 the next ring, etc towards the edge (5 or 6 rings?), then make the rings beyond the disc Z = 7,8,9 etc…
Then lighting a ring is trivial: just light all matching Z.

I’m really curious how fast atan2/hypot is compared to a cached version (Mapped would be faster, but at the cost of XYZ, I agree polar is currently much lesser used.)

In this particular case, I think having things like “arms” and “rings” as precalced arrays (or tricks like tweaking Z above) will give way more flexible and fast patterns especially for sound reactivity. But that’s specific to this item, not in general. Every art piece is going to have optimizing for it’s layout. Even a house layout could benefit, if you had “windows” or “columns” or whatever.

We really lack a quick easy way to fill arrays, since we can’t do array = [1,2,3…]
Since we know the index #s, that would enable a short and easy way to populate data like those.

[zranger1]

Here’s mapper code that generates one or more of those spirals on the fly. This lets you control the scaling and spacing, plus it’d be pretty easy to add cones or rings around the outside this way.

function (pixelCount) {
  var map = []
  
  buildFermatSpiral(-5,0,.6,pixelCount/2,map)
  buildFermatSpiral(5,0,.6,pixelCount/2,map) 
  
// fake extra pixels added to map to set the bounds of the
// coordinate space so the normalizer preserves aspect ratio
  var scale = 10;
  map.push([-scale,-scale])
  map.push([scale,scale])
  
  return map;
}

function buildFermatSpiral(originX, originY, spacing, pixelCount,map) {

  for (var i = 0; i < pixelCount; i++) {
    r = spacing * Math.sqrt(i);
    theta = i * 2.3998277   // golden angle
    
    y = originY - (r * Math.sin(theta));
    x = originX + (r * Math.cos(theta));
    map.push([x, y])    

  }
}

[Sunandmooncouture]

@wizard

Do you intend to have both sides mapped, or mirroring data?

the hope was to map both sides. however, the way it’s currently wired is a mess. I was so excited to get it assembled I didn’t think about mapping while wiring.

the data starts at the right F64, then goes to the bottom cylinder and spirals up towards the F64. The data then crosses to the other side, and into the second F64 then bottom of cylinder, spiraling up to the top.

I should have definitely come out of the F64 and gone top-down instead of bottom up.
Also, on the other side it probably should have started at the bottom of the cylinder then ended at the F64. That would allow for a single map of a cylinder object (with cone tops?) as recommended above.

The simplest thing would be to just split the data out into 2 lines, and have them both start at each F64 then spiral down the sides. I may start there for easiest mapping, and make another one later with the more complex full cylinder (I’ll be making a few of these, and Jason’s fabricating some custom sizes just for me!)

as for mapping
I got the polar radius mapping from the spreadsheet and it looks just like the videos Jason posted.
Thanks @JasonCoon !

Still not sure how I want to incorporate the sides of the can. Each of the 6 rows has 35 LEDs. The easiest way would be use the online mapping tool, and just draw concentric circles extending beyond the F64 of 35 pixels each. But that’s using a 2D map and wouldn’t allow for any 3D patterns. I like the idea of a cone/cylinder but the math is a little beyond me for now (atan2 and hypot3 ::whoosh: so that might be a later version too.

[Scruffynerf]

that wiring is awkward, but totally mappable, especially thanks to @zranger’s code.

We’ll help get you a decent map, math degree not required.

The code above will do the discs. Something like this will do the rings…

function rings(loops, ledcount) {  // so ledcount should be 6*35, loops should be 6
  for (i = 0; i < ledcount; i++) {
    c = i / ledcount * Math.PI * 2 * loops
    map.push([Math.cos(c), Math.sin(c), floor(i/35))
  }
}

You likely will have to play a bit with the start spot, to get it to line up with where the ring starts. That also will number them Zwise in one direction, you might want to reverse or add a nudgefactor for the disc Zs.

so you’d call a disc, a ring, a disc, a ring, given your wiring. And if the rings going toward the discs, you might need to go counterclockwise, or change the Zs, in addition to the initial angle issue. But all of that is easy to tweak.

[Sunandmooncouture]

I redid the wiring so it’s right F64 > right spiral top down > left spiral bottom up > F64.
the arrows on both spirals all point the same direction.
should be way easier to map. at least KITT looks a lot better even without a map.
I’ll take a look at the mapping options mentioned above later tonight. lots of research to do.

[Sunandmooncouture]

ok we’re getting somewhere

The buildFermatSpiral doesn’t match the mapping of the actual F64 layout. I think next approach is instead of using a function just map.push the array from Jason on both ends, maybe insert a slight Z. work in progress, thanks for everyone’s help getting this far!

function (pixelCount) {
    var map = []
    var zend = 0
    var xoffset = 0
    var offset = false
    
    // map F64
    zend = 0
    if(offset) {xoffset = -5}
    buildFermatSpiral(xoffset,0,.2,64,map, zend)

    // map helix connecting each F64
    var helixCount = (pixelCount-128);
    zend = buildHelixMap(helixCount, map, zend)

    // map F64
    if(offset) {xoffset = 5}
    buildFermatSpiral(xoffset,0,.2,64,map, zend) 
    
  // fake extra pixels added to map to set the bounds of the
  // coordinate space so the normalizer preserves aspect ratio
    var scale = 2;
    if(offset) {scale = 6}
    map.push([-scale,-scale, 0])
    map.push([scale,scale, zend])
    
    return map;
  }
  
  function buildFermatSpiral(originX, originY, spacing, pixelCount,map, zend) {
  
    for (var i = 0; i < pixelCount; i++) {
      r = spacing * Math.sqrt(i);
      theta = i * 2.3998277   // golden angle
      
      y = originY - (r * Math.sin(theta));
      x = originX + (r * Math.cos(theta));
      map.push([x, y, zend])    
  
    }
  }
  

  function buildHelixMap(pixelCount, map) {
    var loops = 12

    var helixCount = (pixelCount-128);
    var rowCount = helixCount/35;
    var lastZ = 0;
    
    for (i = 0; i < pixelCount; i++) {
      c = i / pixelCount * Math.PI * 2 * loops
      lastZ = i/rowCount;
      map.push([Math.cos(c), Math.sin(c), lastZ])
    }
    
    return lastZ;
  }

[Scruffynerf]

You likely need two slight tweaks on buildFermatSpiral
1 - the spacing, to find the right value of the sizing
2 - the angle it starts at, since it starts at zero, and depending on how you mounted it, relative to where it expects led 0,1,etc… to be. That’s a rotation. You can adjust for that, by adding this:

function buildFermatSpiral(originX, originY, spacing, pixelCount,map, zend, angleoffset) {
   reallocation = [0, 13, 26, 39, 52, 57, 44, 31, 18, 5, 10, 23, 36, 49, 62, 54, 41, 28, 15, 2, 7, 20, 33, 46, 59, 51, 38, 25, 12, 4, 17, 30, 43, 56, 61, 48, 35, 22, 9, 1, 14, 27, 40, 53, 58, 45, 32, 19, 6, 11, 24, 37, 50, 63, 55, 42, 29, 16, 3, 8, 21, 34, 47, 60]
    for (var i = 0; i < pixelCount; i++) {
      r = spacing * Math.sqrt(reallocation[i]);
      theta = reallocation[i] * 2.3998277 + angleoffset   // golden angle
      y = originY - (r * Math.sin(theta));
      x = originX + (r * Math.cos(theta));
      map.push([x, y, zend])    
    }
  }

you can measure it, or just play until it lines up right. angleoffset would be in radians, so measure the angle compared to ‘0’.

[Sunandmooncouture]

The function as is maps each pixel in order from inner spiral to outer spiral, almost like concentric rings.
The actual physical LEDs are mapped one arm at a time, from center to edge then the next arm edge to center.
If you refer back to the first post with the online map tool.
I’m not convinced the physical led placement can perfectly align with a mathematical formula, due to probably constraints in PCB design.
For example, the jump from 33 to 34 or 43 to 44 doesn’t seem to match the other arms, same with the jump from 0 to 1, vs 20 starting so far out.
I could be totally off, I admit I don’t understand the math well enough yet.
Maybe @JasonCoon can chime in here?
I can give it a shot, but I still think starting with the static map would be easier.