Mapping examples - share yours!

Patterns and Code
,
1

Given the number of maps, attempted maps, misunderstood maps, and so on, it might make sense for a “map repo” to happen, perhaps here in the forum, perhaps similar to the pattern library. (In the repo is a good idea, but I fear those who need it most won’t find it there)

If it’s formatted correctly, with an attachment photo showing the map, and either the code or the coordinates in a summary (format as code, then format as summary, so it’s hidden otherwise), maybe the forum can be the start for this.

Code can often be useful to see how to write mapping code. Coordinates are less useful but they also can help newbies learn how this all works and help them see how maps make sense.

I’ll try and link some later, unless someone else beats me to it.

2 Likes
2

Nice idea! A lot of my map code is absolute trash though that I’m ashamed to share, ha.

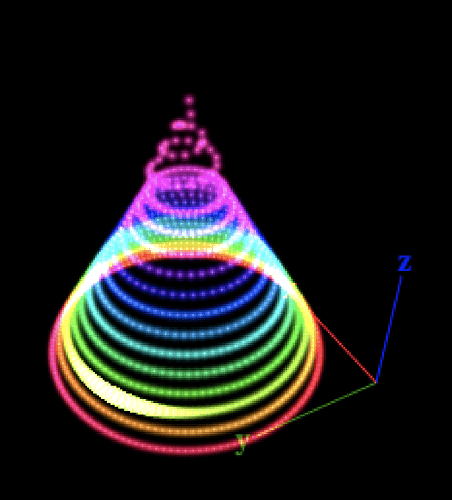
I’ll start off with my tree map for this year, which I’ve added a few comments to. I have an artificial tree I wired “permanently”, so I model it as rings except for the very top, which is a spiral cone.

ChristmasTree 2021-12-05 09-21-06
ChristmasTree 2021-12-05 09-21-06990×1094 65.1 KB

This map gets me some OK-isy result for +/- 10% X,Y,Z:

Here's the code (click to expand) 
function (pixelCount) {
  var map = []
  
  // Flat ring generator
  function ring(pixels, r, h, start) {
    for (j = 0; j < pixels; j++) {
      c = j / pixels * Math.PI * 2;
      point = [r * Math.cos(c - start), r * Math.sin(c - start), h]
      map.push(point)
    }
  }
  
  // Wizard's spiral cone generator
  function cone(cpixels) {
    loops = 3
    r = 4
    phase = 0
    pixelSpacing = 1.3
    resolution = .00005 //controls the resolution of the integral
    a = Math.PI * 2 * loops
    
    function conicalHelix(t, r, a) {
      z = layerPixels.length +130*t/cpixels
      x = (1-t) * r * Math.cos(t * a - phase * Math.PI * 2)
      y = (1-t) * r * Math.sin(t * a - phase * Math.PI * 2)
      return [x,y,z]
    }
    
    function conicalHelixArcLength(t1, t2, r, a) {
      h1 = conicalHelix(t1, r, a)
      h2 = conicalHelix(t2, r, a)
      dh = [h1[0] - h2[0], h1[1] - h2[1], h1[2] - h2[2]]
      return Math.sqrt(dh[0]*dh[0] + dh[1]*dh[1] + dh[2]*dh[2])
    }
    
    for (t = 0, i = 0; i < cpixels; i++) {
      //integrate arc lengths until we cover the distance to our next pixel
      l = 0;
      while (l < pixelSpacing) {
        l += conicalHelixArcLength(t, t+resolution, r, a)
        t += resolution
      }
      map.push(conicalHelix(t, r, a))
    }
  
  }
  
  // Number of pixels in each ring layer
  var layerPixels = [134, 122, 114, 
                      96, 84, 79, 68, 
                      73, 49, 40, 41, 37,
                      33];
  // Angular starting offset for each layer
  var layerAngles = [  -0.02,  0.02,  0.13,
                       -.08, -.07, 0.03, 
                       0.05, -.08, -.05, 0.04, .1, -.66, 
                       0.6];

  // For each layer
  for (i = 0; i < layerPixels.length; i++) {
    ring(layerPixels[i],              // pixels
         layerPixels.length - i + 3,  // radius - gets smaller each layer, but min radius of 3
         i,                           // height
         layerAngles[i] * Math.PI * 2); // angular offset
  }
  cone(30) // top is a simple spiral
  return map
}
1 Like
3

So the maps should be inserted at the beginning of the pattern code correct?
Twilight

4

No, the only place to do a map is the mapping tab. (And yes, it only saves one map) It’s not the same sort of code as a pattern.

6

I’m building a few light modules that have LEDs arrayed offset from the previous line and I coded this mapper that creates the appropriate mapping for a hexagon shape, and also reverses direction every row due to how the strips are wired up.

this mapper ignores the pixelCount parameter in favor of a explict declaration of the edge length…

image
image944×942 92.5 KB 

function (pixelCount) {
  // call reverse if your layout is from bottom and up
  var reverseMap = true;

  // final map to export
  var map = [];
  
  // configuration of hex 
  var side = 8;
  var shapeHeight = side * 2 - 1;
  var shapeWidth = shapeHeight * 2 - 1;
  
  for (r = 0; r < shapeHeight; r++) {
	var isEvenRow = r % 2 == 0;
	var isIncreasing = r < side;
	var offset = 0;
	var width = 0;
	
	if (isIncreasing) {
	  offset = side - r;
	  width = side + r;
	} else {
	  offset = (r + 2) - side;
	  width = (shapeHeight) - offset + 1
	}
	
	for (c = 0; c < width; c++) {
	  if (isEvenRow) {
		var pushX = (c * 2) + offset
	  } else {
		var tempX = (c * 2) + offset
		var pushX = shapeWidth - tempX + 1
	  }
	  var pushY = r;
	  
	  map.push([pushX, pushY]);
	}
  }
  
  if (reverseMap) {
	return map.reverse()
  } else {
	return map
  }
}
3 Likes
7

OK, that’s one question down. If you add a map under the mapping tab, is it linked to the program you are editing at the time? Does it persist if you switch programs?

If no, then let’s say you added a 2D map when editing program “myprogram2D”. Then you open “myprogram1D”, or “myprogram 3D”. Will “myprogram1D” ignore it and “myprogram3D” not run and ask for a proper map?

If it only saves one map at a time do you have to cut and paste maps from a text file?

8

No, there is only one map. It’s not expected that you will change your physical config and need more than one. If you put in a 3D map, and run a 2D map using program that doesn’t have a render3D() function, it’ll just use X and Y (first two values).

See other discussions on this forum re this topic.

9

That makes sense. Thanks