I just reviewed the code and added a bunch of comments. Let me know if anything is unclear. I might have over-optimized because it started getting slower.
The one thing I am still trying to get right is the gamma of the antialiased pixels. These WS2812 LEDs are eye-searingly bright so when I turn them down to a safe level I am down to only a few bits of color depth. I am thinking of pasting my own HSVtoRGB in here so that I can use v=a*a in PixelMax() instead of multiplying r,g,b separately but other ideas are of course most welcome!
Come to think of it I could do the squaring at render time for a little speedup … but I’ll let y’all at it first!
// This pattern creates a rectangular framebuffer
// and does its own integer coordinate mapping
// and draws a digital clock
// with morphing digits
// using Xiaolin Wu's antialiased line algorithm.
var blur = 0
export function sliderMotion_Blur(v) {
blur = v * 0.9
}
// Duplicate PixelBlaze 'Mapper' functionality without normalizing
var width = 32
var height = 8
var coordmap = array(pixelCount)
for (index=0; index<pixelCount; index++) {
x = floor(index / height)
y = index % height
y = x % 2 == 1 ? height - 1 - y : y // I have a zigzag 32x8 LED matrix
coords = array(2)
coords[0] = x
coords[1] = y
coordmap[index] = coords
}
// RGB framebuffer
// ... Storage
var Pr = array(width); for (i=0; i<width; i++) Pr[i] = array(height)
var Pg = array(width); for (i=0; i<width; i++) Pg[i] = array(height)
var Pb = array(width); for (i=0; i<width; i++) Pb[i] = array(height)
// ... Render a pixel
// - Only used by WuLine, so we do 'alpha' here to keep WuLine readable
// - Uses max() so overlapping line pixels don't make bright spots
function PixelMax(x,y,a,r,g,b) {
//x = floor(x)
//y = floor(y)
a = a*a // gamma somethingsomething?
if (x >= 0 && x < width && y >= 0 && y < height) {
Pr[x][y] = max(Pr[x][y], clamp(r*a, 0, 1))
Pg[x][y] = max(Pg[x][y], clamp(g*a, 0, 1))
Pb[x][y] = max(Pb[x][y], clamp(b*a, 0, 1))
}
}
// Xiaolin Wu's antialiased line algorithm
// Adapted from https://gist.github.com/polyamide/3f33cb4dc69e22fbf8b66cee39b78d60
// (replaced utility functions with PixelBlaze built-ins)
function WuLine(x0, y0, x1, y1, r, g, b) {
if (x0 == x1 && y0 == y1) return
steep = abs(y1 - y0) > abs(x1 - x0);
if (steep) {
tmp = y0; y0 = x0; x0 = tmp;
tmp = y1; y1 = x1; x1 = tmp;
}
if (x0 > x1) {
tmp = x0; x0 = x1; x1 = tmp;
tmp = y0; y0 = y1; y1 = tmp;
}
dx = x1 - x0;
dy = y1 - y0;
gradient = dy / dx;
xEnd = round(x0);
yEnd = y0 + gradient * (xEnd - x0);
xGap = 1 - frac(x0 + 0.5);
xPx1 = xEnd;
yPx1 = trunc(yEnd);
if (steep) {
PixelMax(yPx1, xPx1, 1 - frac(yEnd) * xGap, r, g, b )
PixelMax(yPx1 + 1, xPx1, frac(yEnd) * xGap, r, g, b )
} else {
PixelMax(xPx1, yPx1, 1 - frac(yEnd) * xGap, r, g, b )
PixelMax(xPx1, yPx1 + 1, frac(yEnd) * xGap, r, g, b )
}
intery = yEnd + gradient;
xEnd = round(x1);
yEnd = y1 + gradient * (xEnd - x1);
xGap = frac(x1 + 0.5);
xPx2 = xEnd;
yPx2 = trunc(yEnd);
if (steep) {
PixelMax(yPx2, xPx2, 1 - frac(yEnd) * xGap, r, g, b )
PixelMax(yPx2 + 1, xPx2, frac(yEnd) * xGap, r, g, b )
} else {
PixelMax(xPx2, yPx2, 1 - frac(yEnd) * xGap, r, g, b )
PixelMax(xPx2, yPx2 + 1, frac(yEnd) * xGap, r, g, b )
}
if (steep) {
for (x = xPx1 + 1; x <= xPx2 - 1; x++) {
PixelMax(trunc(intery), x, 1 - frac(intery), r, g, b )
PixelMax(trunc(intery) + 1, x, frac(intery), r, g, b )
intery = intery + gradient;
}
} else {
for (x = xPx1 + 1; x <= xPx2 - 1; x++) {
PixelMax(x, trunc(intery), 1 - frac(intery), r, g, b )
PixelMax(x, trunc(intery) + 1, frac(intery), r, g, b )
intery = intery + gradient
}
}
}
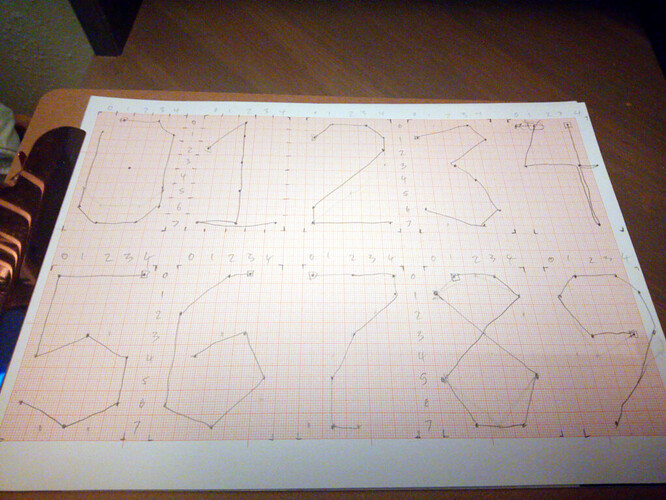
// Digit data - 5x8 pixels
// - each digit is 7 sequential lines
// represented by a list of 8 x,y coordinates
var Digits = array(10)
for (i=0;i<10;i++){
Digits[i]=array(8)
for (j=0;j<8;j++){
Digits[i][j]=array(2)
}
}
Digits[0][0][0] = 1
Digits[0][0][1] = 0
Digits[0][1][0] = 3
Digits[0][1][1] = 0
Digits[0][2][0] = 4
Digits[0][2][1] = 1
Digits[0][3][0] = 4
Digits[0][3][1] = 6
Digits[0][4][0] = 3
Digits[0][4][1] = 7
Digits[0][5][0] = 1
Digits[0][5][1] = 7
Digits[0][6][0] = 0
Digits[0][6][1] = 6
Digits[0][7][0] = 0
Digits[0][7][1] = 1
Digits[1][0][0] = 0
Digits[1][0][1] = 2
Digits[1][1][0] = 2
Digits[1][1][1] = 0
Digits[1][2][0] = 2
Digits[1][2][1] = 1
Digits[1][3][0] = 2
Digits[1][3][1] = 3
Digits[1][4][0] = 2
Digits[1][4][1] = 5
Digits[1][5][0] = 2
Digits[1][5][1] = 7
Digits[1][6][0] = 0
Digits[1][6][1] = 7
Digits[1][7][0] = 4
Digits[1][7][1] = 7
Digits[2][0][0] = 0
Digits[2][0][1] = 1
Digits[2][1][0] = 1
Digits[2][1][1] = 0
Digits[2][2][0] = 3
Digits[2][2][1] = 0
Digits[2][3][0] = 4
Digits[2][3][1] = 1
Digits[2][4][0] = 4
Digits[2][4][1] = 2
Digits[2][5][0] = 0
Digits[2][5][1] = 6
Digits[2][6][0] = 0
Digits[2][6][1] = 7
Digits[2][7][0] = 4
Digits[2][7][1] = 7
Digits[3][0][0] = 0
Digits[3][0][1] = 1
Digits[3][1][0] = 2
Digits[3][1][1] = 0
Digits[3][2][0] = 4
Digits[3][2][1] = 1
Digits[3][3][0] = 2
Digits[3][3][1] = 3
Digits[3][4][0] = 3
Digits[3][4][1] = 4
Digits[3][5][0] = 4
Digits[3][5][1] = 6
Digits[3][6][0] = 2
Digits[3][6][1] = 7
Digits[3][7][0] = 0
Digits[3][7][1] = 6
Digits[4][0][0] = 3
Digits[4][0][1] = 0
Digits[4][1][0] = 3
Digits[4][1][1] = 3
Digits[4][2][0] = 4
Digits[4][2][1] = 3
Digits[4][3][0] = 3
Digits[4][3][1] = 3
Digits[4][4][0] = 3
Digits[4][4][1] = 7
Digits[4][5][0] = 3
Digits[4][5][1] = 3
Digits[4][6][0] = 0
Digits[4][6][1] = 3
Digits[4][7][0] = 0
Digits[4][7][1] = 0
Digits[5][0][0] = 4
Digits[5][0][1] = 0
Digits[5][1][0] = 0
Digits[5][1][1] = 0
Digits[5][2][0] = 0
Digits[5][2][1] = 4
Digits[5][3][0] = 2
Digits[5][3][1] = 3
Digits[5][4][0] = 4
Digits[5][4][1] = 4
Digits[5][5][0] = 4
Digits[5][5][1] = 6
Digits[5][6][0] = 2
Digits[5][6][1] = 7
Digits[5][7][0] = 0
Digits[5][7][1] = 6
Digits[6][0][0] = 3
Digits[6][0][1] = 0
Digits[6][1][0] = 2
Digits[6][1][1] = 0
Digits[6][2][0] = 0
Digits[6][2][1] = 2
Digits[6][3][0] = 0
Digits[6][3][1] = 6
Digits[6][4][0] = 2
Digits[6][4][1] = 7
Digits[6][5][0] = 4
Digits[6][5][1] = 5
Digits[6][6][0] = 3
Digits[6][6][1] = 3
Digits[6][7][0] = 1
Digits[6][7][1] = 3
Digits[7][0][0] = 0
Digits[7][0][1] = 0
Digits[7][1][0] = 2
Digits[7][1][1] = 0
Digits[7][2][0] = 4
Digits[7][2][1] = 0
Digits[7][3][0] = 4
Digits[7][3][1] = 1
Digits[7][4][0] = 2
Digits[7][4][1] = 3
Digits[7][5][0] = 1
Digits[7][5][1] = 5
Digits[7][6][0] = 1
Digits[7][6][1] = 7
Digits[7][7][0] = 2
Digits[7][7][1] = 7
Digits[8][0][0] = 1
Digits[8][0][1] = 0
Digits[8][1][0] = 3
Digits[8][1][1] = 0
Digits[8][2][0] = 4
Digits[8][2][1] = 1
Digits[8][3][0] = 0
Digits[8][3][1] = 5
Digits[8][4][0] = 1
Digits[8][4][1] = 7
Digits[8][5][0] = 3
Digits[8][5][1] = 7
Digits[8][6][0] = 4
Digits[8][6][1] = 5
Digits[8][7][0] = 0
Digits[8][7][1] = 1
Digits[9][0][0] = 3
Digits[9][0][1] = 3
Digits[9][1][0] = 1
Digits[9][1][1] = 3
Digits[9][2][0] = 0
Digits[9][2][1] = 1
Digits[9][3][0] = 1
Digits[9][3][1] = 0
Digits[9][4][0] = 3
Digits[9][4][1] = 0
Digits[9][5][0] = 4
Digits[9][5][1] = 1
Digits[9][6][0] = 4
Digits[9][6][1] = 3
Digits[9][7][0] = 1
Digits[9][7][1] = 7
// lerp is used on the line ends to morph the digits
function lerp(t,a,b){
return a*(1-t)+b*t
}
// Draw a Digit
// - starting at x,y
// - morph each line end between d1,d2 using t (0..1)
// - draw WuLine with r,g,b
function DrawDigit(x,y,dd1,dd2,t,r,g,b) {
d1 = Digits[dd1]
if (dd1==dd2) { // skip lerp if digits are the same
for (L=0;L<7;L++) {
WuLine(
x + d1[L][0],
y + d1[L][1],
x + d1[L+1][0],
y + d1[L+1][1],
r, g, b
)
}
} else {
d2 = Digits[dd2]
for (L=0;L<7;L++) {
WuLine(
x + lerp(t,d1[L][0],d2[L][0]),
y + lerp(t,d1[L][1],d2[L][1]),
x + lerp(t,d1[L+1][0],d2[L+1][0]),
y + lerp(t,d1[L+1][1],d2[L+1][1]),
r, g, b
)
}
}
}
// Render-related variables persistent between frames
export var lastsecond = -1
export var ms = 0
// Clear (or fade if blur enabled) framebuffer
// and render the current time
export function beforeRender(delta) {
for (i=0; i<width; i++) {
for (j=0; j<height; j++) {
Pr[i][j] = blur * Pr[i][j]
Pg[i][j] = blur * Pg[i][j]
Pb[i][j] = blur * Pb[i][j]
}
}
// Extract digits for each part of current time
// and next time unit with 'n' prefix
// (e.g. 'nm2' is second digit of next minute)
// and collect milliseconds from delta in 'ms'
hour = clockHour()
h2 = hour % 10
h1 = (hour - h2)/10
nexthour = (hour + 1) % 24
nh2 = nexthour % 10
nh1 = (nexthour - nh2)/10
minute = clockMinute()
m2 = minute % 10
m1 = (minute - m2)/10
nextminute = (minute + 1) % 60
nm2 = nextminute % 10
nm1 = (nextminute - nm2)/10
second = clockSecond()
s2 = second % 10
s1 = (second - s2)/10
nextsecond = (second + 1) % 60
ns2 = nextsecond % 10
ns1 = (nextsecond - ns2)/10
if (second == lastsecond) {
ms = clamp(ms + delta, 0, 1000)
} else {
ms = 0
lastsecond = second
}
// transition to next second digit
// with wave transition around (0.1 .. 0.9)
// hint: 1000 / 1428.57142 =~ 0.7
ts = clamp( wave(clamp(ms/1428.57142-0.1,0,1)-0.25), 0,1)
tm = second == 59 ? ts : 0
th = (second == 59 && minute == 59) ? tm : 0
// Rainbow digits because they are right next to each other
DrawDigit(0,0,h1,nh1,th,1,0,0)
DrawDigit(5,0,h2,nh2,th,1,1,0)
DrawDigit(11,0,m1,nm1,tm,0,1,0)
DrawDigit(16,0,m2,nm2,tm,0,1,1)
DrawDigit(22,0,s1,ns1,ts,0,0,1)
DrawDigit(27,0,s2,ns2,ts,1,0,1)
// draw pulsing white 'second' dots in remaining 2 columns
br = (1-ms/1000)
Pr[10][1] = br
Pr[10][2] = br
Pr[21][1] = br
Pr[21][2] = br
Pr[10][5] = br
Pr[10][6] = br
Pr[21][5] = br
Pr[21][6] = br
Pg[10][1] = br
Pg[10][2] = br
Pg[21][1] = br
Pg[21][2] = br
Pg[10][5] = br
Pg[10][6] = br
Pg[21][5] = br
Pg[21][6] = br
Pb[10][1] = br
Pb[10][2] = br
Pb[21][1] = br
Pb[21][2] = br
Pb[10][5] = br
Pb[10][6] = br
Pb[21][5] = br
Pb[21][6] = br
}
// Draw from the framebuffer
export function render(index) {
coords = coordmap[index]
x = coords[0]
y = coords[1]
rgb(Pr[x][y], Pg[x][y], Pb[x][y])
}



 ). As with all such projects, all it requires is a pencil and paper …
). As with all such projects, all it requires is a pencil and paper …