I suspect a Tixy function is mostly trivial for PB.
The 0-15 values need to be adjusted for the 0…1 values of PB, T will be adjusted perhaps, and negative values going red (or whatever).
But it’s neat and for newbies who don’t quite grasp how math patterns can be used, this is a good starting point, with just one line to understand.
For sure!
These are some other minimalist graphical math heavy systems that were inspiration for PB:
Some more Tixy (and other math/graphic) links.
If nobody beats me to it, I’ll have to do a Tixy pattern for PB. So many good patterns including Mandelbrot zooms, Conway Life, text scrollers, fire, and more. Considering how small most are (one line of JavaScript), you could easily pack dozens into a single PB pattern.
Tixy related:
Twitter search, cause so many good patterns
https://mobile.twitter.com/search?q=Tixy.land
3d:
Hidef:
Non-tixy:
So I got a basic Tixy clone working despite a storm related power outage at home. I grabbed the new 16x16 matrix, a PB, 10a power supply, and my laptop and went to my in-laws (much warmer). I adjust the white to be bluish, but that’s just a setting anyway. Some examples needed hypot(), but that’s an easy function to add. A few used arrays, and I’ll have to play with those more. I also need to add a gamma correction to make the low levels of light easier to notice.
I’ll post it tomorrow, if I get power back. It’ll work on smaller matrixes too since the map just works as expected.
Taking a break, then I’m going to add a full color mode, so instead of white for any positive value and red for negative values where size of the value is used as brightness, I’ll use the value as the hue.
I’ve just uploaded to the electromage pattern repo an alpha of my Tixy pattern. It’s functional but I’ll be adding more formulas (there are only 60 now…) to it, as well as bug fixes and more comments, etc. It’ll also be on GitHub. New formulas welcomed gladly. Documentation for how tixy.land works in the first handful of formulas in the commented code. (Or visit tixy.land itself, same documented walk thru there, slightly different order of later examples)
And of course as soon as I pull the trigger, I see bugs to fix. It starts on pattern 15, cycles every 3 seconds (should be longer or adjustable), and won’t start over once it hits 60. Oops.
I was debugging the Mondrian pattern. @wizard, I am correct that that’s a math overflow causing the corners to not be solid? (Also appears on moving cross formula, similarly). It’s multiplying two small numbers, I wouldn’t think it was too big but…
Just downloaded and played with this. It looks good, and shows a bunch of really cool things you can do with just a little math. Nice!!
(and yeah, could use a pattern = pattern % numPatterns or something like that in there – I got hypnotized watching the whole thing, so was actually kind of glad it didn’t start over that first time…)
Yeah, exactly, I meant to add that before upload but…
and will probably add a “greatest hits option” that only cycles thru a select group (array of which ones) so you can pick and choose your favorites, and just get those cycling. Given that I expect easily over 100 patterns
I’m enjoying the challenge of porting some, due to PBs limited language that isn’t 100% JavaScript complete, for example, no on the fly arrays, no .map, limited assignments, etc. I want to get the mandelbrot, life, space invader, and some others working, plus every day I see a few new ones.
I’ll be making a demo video for this, I think, once I’m happy with the basics.
I also plan on adding R/Polar support, for more “swirly” patterns. (Thrixy ? Adding Th+R). And I still need to build my 3D and add 3D support.
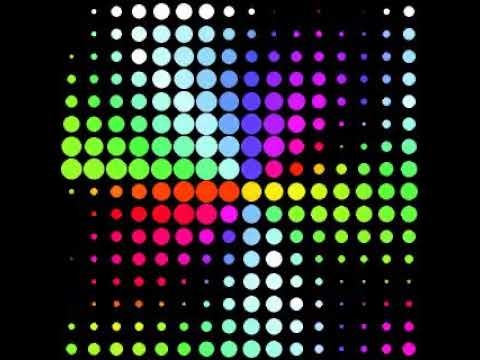
@Scruffynerf,
Neat! Fun!
If you are looking for an accurate replica, I tweaked the render function to more closely match tixy’s for mono mode.
export function render2D(index,xo,yo) {
x = floor(xo * 16)
y = floor(yo * 16)
result = tixy[pattern](t1,index,x,y);
if (MonoOrColor) { //Color
h = result * ColorShift;
v = abs(result) + BrightShift
hsv(h,1,v)
} else { // Mono
if (result < 0) {
result = -result
h = Negative
} else {
h = Positive
}
v = clamp(result , 0, 1) //clamp to range
hsv(h,1,v*v)
}
}
They take the result and scale it up to a radius, clamping to max size. The result’s already in an appropriate scale in our case, but should still clamp before squaring to avoid overflows. I square for better detail at the low end, instead of cube it.
In some places, tixy uses sneaky side effects to reduce character count. This is a good example in moving cross:
(y-4*t|0) * (x-2-t|0)
The bitwise or | happens last, and in JavaScript implicitly converts the number to a 32 bit signed integer. In Pixelblaze, this doesn’t happen and you get a bitwise or across the whole number.
For positive numbers, floor does the same thing, but it makes negative numbers more negative, unlike bitwise OR with 0. You can’t just logical AND away the fractional bits on a fixed point negative number either (removing them makes negative numbers more negative, two’s compliment and all that).
This can do the trick:
function toInt(v) {
return v - (v % 1)
}
Applying this to the moving cross pattern:
toInt(y-4*t) * toInt(x-2-t)
Gives similar results to tixy (2 pixel wide bars).
BTW, Pixelblaze supports the same lambda expressions as JS / tixy.
tixy[10] = (t,i,x,y) => { return y - x }; // simple triangle
Can be written like this as well
tixy[10] = (t,i,x,y) => y - x // simple triangle
Oh excellent, so I can clean up a lot of code. Thanks.
Thanks for clarifying lots of small bits about how PB as a language/parser works!
It looks like even in PB, double tilde does the same as your toInt… Yes? (I haven’t tested it fully but I see a case where it looks like it is)
Two NOT bitwise operators in a row?
I just played with this a bit… I don’t have an easy way to see bit values for the .16 portion, so I can’t see exactly what’s going on, but it looks like ~ only preserves the integer portion.
So you can use that trick to ditch the fractional part on positive numbers, but it doesn’t work quite the same way on negatives. It makes them more negative. For example, ~~1.234 returns 1, ~~ -1.234 returns -2.
If you can live with this, it’s faster than a function call. Though unless I was seriously hurting for fps and it was in a critical inner loop, I’d try never ever to do this in production code. Too likely to be misread later, or to break if somebody ever accidentally “fixed” the interpreter.
@wizard, I was going to ask at some point, but this seems like a good time: Can you consider giving us nice fast whole() and frac() functions to do these jobs?
Interesting, cause this says ~~ shouldn’t do that
I mean it’s not JavaScript, so if it’s equal to floor on PB, that’s fine. I just was curious. If it’s not the same as in JavaScript, worth documenting.
@wizard got another PB logic operator question:
x-=8,y-=8,f=(k)=>hypot(xcos(t+k)+ysin(t+k),xsin(t+k)/2-ycos(t+k)/2)/4<1,f(0)^f(-1.05)^f(1.05)
even after some rewriting, I realized the issue is the end:
a^b^c
that’s using ^ as XOR, but I think it’s doing exponent on PB, since I’ve been using that elsewhere…
so what is the bitwise XOR operator on PB?
3D Tixy… Meaning a 3D map on PB could do this…
pretty sure ^ is XOR on PB – we used a lot of it when messing around with the XORShift PRNG back in a couple of the early exercises.
I’ll have to play with that one again. I have a handful of tixy lines to port over collected and should scour the net for newer ones too. Time for TixyPB 2.0.
So the guy behind G’MIC added tixy support to gmic
And then he did it one better, he added a Z that is a complex number represented by x+iy (that i is the squareroot of -1, not pixel index, so really he used j for clarity)
In this case he’s using Z this way:
If you have a complex number, x+iy, it can also be expressed by a polar conversion, which yields a radius and angle. The radius is used to define the size of the circle (which for PB purposes is akin to brightness) and the angle is used to define color by hue.
This is brilliant and I really want to add this to my tixy Port. But of course that means adding complex number support to do it right.
Coming soonish hopefully.
well, hot damn, I’m 90% done with the core of the port of complex.js to PB, still testing, but I’ve got some nice patterns already, just testing my complex functions.
This is a game changer, I think. I’m limiting it to a fixed 2 element array (real, and imaginary), to keep it within PB language limits.
one gotcha I found in porting this, recording so others might find it helpful:
if you try to use ===, you get an error
“Cannot read property ‘stack’ of undefined”
No pointer to where the error is, it’s just a blocker, can’t save the pattern, etc.
Search for ===, and replace with == (which should work most of the time)